ブログマスターの「ライズ」です。”Slip Tips” 4回目の投稿です。
現在の投稿テーマは,「円弧すべり解析の最小安全率って何?」です。
今回は,「円弧すべり試行計算」について解説します。
斜面安定解析の一手法として,「円弧すべり探索」,「円弧すべり試行計算」,あるいは「繰り返し円弧すべり計算」などと呼ばれる解析手法があります。これらは,ほぼ同じ解析方法の総称で,「すべり面を円弧と仮定した安定解析による繰り返し試行計算」のことを指します。(”Slip Tips” では「円弧すべり試行計算」と呼びましょう。)
地すべりや急傾斜地の崩壊対策,切土や盛土などの土構造物,擁壁や補強土,仮設山留めや締切りなどの設計に携わったことのある方なら,何度か見聞したことのある解析手法だと思います。実は,斜面設計の現場では頻繁に使用されている手法なんですが,専門書にも,インターネット上にも,具体的な計算方法や結果の利用方法が記載されていません。(どなたかご存知の方がいらっしゃったら,出典を教えてください。お願いします。)
そこで,今回の “Slip Tips” では,「円弧すべり試行計算」の概要を解説し,「最小安全率」を考察するためのバックグラウンドとして,再認識していただこうと思います。
1. 円弧すべり試行計算の意義と目的
まずは,”Slip Tips” 的に円弧すべり試行計算の定義を試みます。
「斜面の2次元断面モデルにおいて,すべり面を円弧形状と仮定し,同円弧の中心座標と半径を様々に変化させて,安定解析を実施する。これらの解析結果群の中から,必要な情報を抽出し,斜面の安定性を評価する指標として,あるいは対策工の設計外力として利用する解析手法。」
概ね以上のような内容でしょうか。
ここでいう「・・・安定解析を実施する。・・・」の安定解析は,前回の “Slip Tips” でも触れた「Fellenius法」,「修正Fellenius法」,「Bishop法」,あるいは「Morgenstern & Price法」などの安定解析式の総称を言います。つまり,円弧すべり試行計算は,「○○法」に則った解析結果を利用することが命題なのではなく,それらの安定解析式を使用した繰り返し試行計算を行い,対象斜面の不安定化の可能性(あるいは危険性)を総当たりにチェックしておこう,というのが主たる目的です。簡単に言ってしまえば,土圧の計算手法として周知されている「試行くさび法」の円弧すべりバージョンみたいのものです。
ここで,「どうして円弧すべりなんだろう?」,「直線すべりや任意形状のすべりは対象としないのか?」という疑問が湧きますよね。ライズも疑問です。この疑問に対して,明確な回答を持っていらっしゃる方は,いないと思います。ですが,ライズなりに想像を膨らませて考えてみました。
【理由その1】
斜面に発生するすべり面は,2次元断面上では下に凹んだ船底状を呈していることが多く,円弧で近似しやすい。
【理由その2】
円弧は,中心座標と半径の2つの情報を設定すれば,形状を規定できる。例えば,円弧の中心座標を地表から遠く離れた位置に置き,半径を大きく取れば,直線形状に近いすべり面をモデル化できる。少ない情報量で,様々なすべり面形状を近似できる「円弧」は,非常に便利な解析ツールである。
計算機環境が整っていない時代は,少ない情報量で繰り返し計算が行える,都合の良い形だったんでしょうね。
【理由その3】
斜面安定解析のルーツであり,国内における解析手法のスタンダードとなっている「Fellenius法」は,円弧すべりを対象として,1927年に発表された手法である。また,ライズの知る限りでは,「Bishop法(1955)」も「Spencer法(1967)」も,その対象は円弧すべりであり,安定解析という手法そのものが,円弧すべりを対象として発展してきたようなものである。
当時は,「斜面安定解析」≒「円弧すべり」が主流だったんだと思います。
円弧すべり試行計算が使用され続けている理由は,以上のような解析手法そのものの発展の経緯と,当時の時代背景が大きく影響しているのではないかと思います。
現在は,当時に比べて,計算機環境が飛躍的に向上していますから,非円弧の任意形状すべりの試行計算を,個人がPC上で行うことも可能ですし,過静定問題で非難され続けてきた「Fellenius法」は使用せず,厳密解が得られる「Morgenstern & Price法」などの解析手法の適用も容易なはずです。しかし,スタンダードが未だに「1927年」の「円弧すべり」ですから,土木が「経験工学」と呼ばれる所以ですよね。
2. 円弧すべり試行計算の適用分野
円弧すべり試行計算は,すべり面の形状を円弧と仮定すること,そして様々な形状の円弧すべりについて安定解析を実施することが特徴です。したがって,この計算方法の適用範囲は,すべり面を円弧で近似できる,比較的小規模な斜面が対象となります。一方,潜在的なすべり面や,地質構造的な弱面などの存在が把握できている斜面については,そもそも試行計算を行う必要がないので,適用されません。そうすると,適用範囲は,自ずと切土のり面や盛土のり面などの人工斜面に絞り込まれます。切土のり面も盛土のり面も,我々の生活圏の中に位置する斜面ですから,不安定化を招くような不測の事態があってはならない構造物です。崩壊などは以ての外です。そこで,この円弧すべり試行計算を適用し,判断漏れのない設計を実施しよう,というのが主たる使用目的です。
一方,地すべりなどの大規模斜面や,崩壊してしまった斜面,崩壊の兆候が認められる斜面災害では,地質調査によってすべり面の形状を明確にする必要がありますので,試行計算は必要ありませんし,滅多に使用されることはありません。(規模の小さい初生地すべりには適用されることがあります。)
3. 次回の “Slip Tips” は,・・・
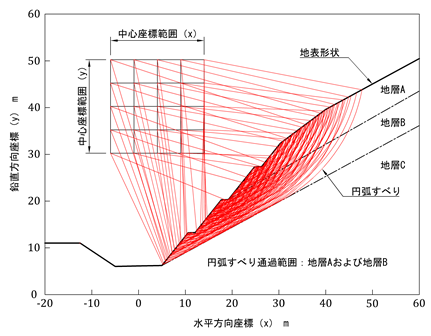
さて,斜面の2次元断面モデルを設定し,円弧すべりの形状を規定する中心座標,半径,円弧の通過範囲などの境界条件を設定すれば,試行計算の結果として,数多くの安定解析結果が得られます。では,これらの中からどの解析結果に注目し,何の指標を持って斜面の安定性を評価すればよいのでしょうか。結論から言いますと,以下の2つの円弧すべりの解析結果が非常に重要となります。(実は,この2つしか使いません。)
「最小安全率すべり」 「最大抑止力すべり」
次回の “Slip Tips” では,上記2つの指標の意義とその利用方法について考察します。
平成26年8月21日 ライズ
[執筆後記]
昨日,平成26年8月20日,広島県広島市安佐南区および安佐北区において,大規模な斜面崩壊と土石流が発生し,多くの方々の尊い生命が失われました。この場を借りて,お亡くなりになられた方,行方不明となっておられる方,怪我を負われた方,お住まいを失われた方,およびご家族の方々に,お悔やみとお見舞いを申し上げます。斜面防災分野の片隅にいるものとして,非常に残念で,悔しい気持ちでいっぱいです。