“Slip Tips” ブログマスターの「ライズ」です。
業務多忙を理由に,“Slip Tips” の更新を2ヶ月以上もさぼっていた,ブログ放置犯です。私なりに,この状況を打開するため,年末年始の休業中に何件かまとめて投稿してしまおう,などと目論んではいたのですが・・・。残念ながら,というか,普段の不摂生がたたったのか,大晦日にインフルエンザを発症し,40°越えの年越しとなってしまいました。“Slip Tips” を気に掛けてくださっている極少数の読者の皆様,お待たせしてすいませんでした。(本当は,ネタ切れです。)
さて,気を引き締めて,“Slip Tips” 新年の再スタートです。
1. 前回までの “Slip Tips” は・・・
前回までの “Slip Tips” では,円弧すべり試行計算について,以下の3つの事項を再認識していただきました。
- 円弧すべり試行計算は,斜面の2次元断面モデルにおいて,様々な形状の円弧すべりを仮定し,それらを対象とする安定解析を実施することで,対象斜面の不安定化の可能性(あるいは危険性)を総当たりにチェックする解析方法である。
- 円弧すべり試行計算では,数多くの安定解析結果が得られる。これらの解析結果群の内,特に重要な解析結果は,「最大抑止力すべり」と「最小安全率すべり」の解析結果である。
- 円弧すべり試行計算の解析結果群の内,計画安全率定義式から導出される必要抑止力 Pr が最も大きい値となる円弧すべりを「最大抑止力すべり」と言い,この Pr 値「最大抑止力」は,グラウンドアンカーや鉄筋挿入などの抑止対策工の設計外力として利用される。
今回の “Slip Tips” は,ブログテーマ「円弧すべり解析の最小安全率って何?」の5回目の投稿です。今回からは,いよいよ(ようやく?)テーマタイトルの「最小安全率」について,その意義と利用方法を考察します。
2. 最小安全率の定義
これまで “Slip Tips” では,「円弧すべり探索」,「円弧すべり試行計算」,「最大抑止力」,「最大抑止力すべり」等々,斜面安定解析に関連する技術用語について,他の文献で明確に定義されていないことを理由に,勝手に定義してきました。それでは,今回のテーマ「最小安全率」や「最小安全率すべり」は,どうかというと・・・。やっぱり,他文献の明確な定義は見当たりません。(斜面関連の技術用語って,なんでこんなにいい加減なんでしょう。) そこで,今回も「最小安全率」と「最小安全率すべり」について,“Slip Tips” 的な定義を試みます。
「任意に規定した地形条件(地表形状・地層形状など)および地質条件(各地層の単位体積重量・せん断強度など)の下で実施された安定解析の試行計算において,次式で定義される安全率 Fs が最も小さい値となる円弧すべり。」
“Slip Tips” では,上記を「最小安全率すべり」,同すべりの安全率を「最小安全率」と定義します。
【備考】 ライズは,「率」の相対比較を表現するとき,「大・小」を使用すべきか,「高・低」を使用すべきか,よく迷ってしまいます。日本語的には,「高・低」が正しいとは思いますが,“Slip Tips” では,安全率の相対比較を「大・小」で表現することにします。「“最低” 安全率すべり」じゃ,なんだかかっこ悪いですよね。
3. 最小安全率の利用方法
「最小安全率すべり」とその解析結果「最小安全率」は,次のようなケースで利用されています。
3-1 斜面の安定性評価
最も一般的な利用方法は,斜面の安定性を評価する指標として利用されるケースです。 “Slip Tips” では,既に極限平衡法における「安全率」の意義を考察しました。「最小安全率」についても,全く同様のことが言えます。すなわち,円弧すべり試行計算によって算出された安全率の内,「最小安全率」が Fs=1.0 であった場合,対象斜面はぎりぎりで安定を保っている極限平衡状態にあると評価されます。一方,「最小安全率」が Fs>1.0 の場合は,平衡状態~安定状態を保っており,「最小安全率」が Fs<1.0 の場合は,平衡状態を逸脱した不安定な状態と評価されます。総当たり試行計算の解析結果群の中で,最も小さい安全率について評価しているのですから,これ以上に安全側の評価はありません。
3-2 対策工の必要性・妥当性の判断
様々なシチュエーションにおける計画安全率と,円弧すべり試行計算の解析結果「最小安全率」との相対比較から,対策工の必要性と妥当性を判断します。解析対象とする斜面の「最小安全率」が所定の計画安全率を上回っていれば,補強対策は必要ありません。しかし,計画安全率を下回る安全率が算出された場合は,抑制工や抑止工などの対策が必要となります。また,対策工が計画されている斜面において,施工途中の各段階,および完成後~供用中を解析対象とした場合,施工途中の各段階においては,「最小安全率」が短期(仮設)の計画安全率を下回らないこと,同じく完成後~供用中においては,「最小安全率」が長期(本設)の計画安全率を下回らないことを確認し,対策工の仕様の妥当性を判断します。
3-3 崩壊形態・規模の推定
斜面の崩壊形状の推定に,円弧すべり試行計算が利用されることがあります。切土のり面や盛土のり面などの人工斜面では,将来における不測の事態を考慮し,崩壊の危険性とその形状・規模を予察しておくことが必要です。そこで,円弧すべり試行計算を実施し,総当たりの解析結果群の中から,安全率が Fs<1.0 となる円弧すべりがどのように分布しているのか,「最小安全率すべり」がどのような形状を呈するのかを把握し,崩壊形態を推察するための参考資料とします。
3-4 せん断強度の逆算
設計対象斜面の崩壊が懸念される場合は,その崩壊形態を予察し,これに対応する対策工を施す必要があります。このようなケースにおいては,「最小安全率すべり」の解析結果に基づいて,土質定数(すべり面せん断強度)を逆算することが有意義です。一般的な逆算の流れは,以下の通りです。
- 崩壊が懸念される斜面の解析モデルを設定し,崩壊時の安全率と地盤の土質定数を仮定します。
- 円弧すべり試行計算を実施し,「最小安全率」=「上記で仮定した崩壊時の安全率」となる,すべり面のせん断強度を算定します。
- 上記で算定したせん断強度を用いて,設計対象斜面の安定性を,円弧すべり試行計算によって再評価します。
この方法で算定されたすべり面せん断強度は,崩壊時を想定した仮定安全率をぎりぎりで満たす,最小のせん断強度です。したがって,同せん断強度を対策工の設計に利用すれば,最も安全側の設計結果を得ることができます。
4. 最小安全率の利用上の留意点
ここで皆さんに質問です。
【問題】
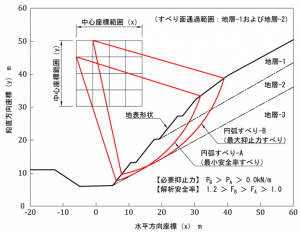
fig.-1 に示すような,同一斜面の円弧すべり試行計算において,「最小安全率すべり A」と「最大抑止力すべり B」という異なる2つのすべり面が算出されました。これらのすべりは,安全率も必要抑止力も異なります。また,安全率については,いずれのすべりも,計画安全率は満たされていませんが,Fs≧1.0 という状況です。このようなケースにおいて,グラウンドアンカーや鉄筋挿入などの抑止対策工を設計する場合,設計対象として A と B どちらのすべりを採用しますか? 以下の解答例を参考に,考えください。
【解答例】
すべり A の安全率が「最小安全率」なのだから,すべり A が最も危険なすべりであり,かつ最も早期に発生するすべりである。同すべりを抑止すれば,最大抑止力すべり B のような大規模な斜面崩壊が発生する前に,地盤の初期変状を抑えることができる。すなわち,最小安全率すべり A を対象とする抑止対策を施せば,すべり B を対象とする大規模な抑止対策を講じる必要はない。最小安全率すべり A を抑止対象とする設計は,対策事業費のコストを抑えることができる最適設計と言える。
・・・・・な~んて考えている方はいませんか?
もっともらしい解答ですが,・・・よ~く考えてくださいね。
これまでの業務の中で,上記のような業務成果を上げている方はいませんよね?
マズいですよ・・・・・・ (;^_^A
最初にお伝えしてしまいますが,
上記の解答例は「誤り」です !! これでは「過小設計」となってしまいます !!
ここで,問題を単純化するため,すべり面の形状を円弧から直線に置き換えて考察してみましょう。
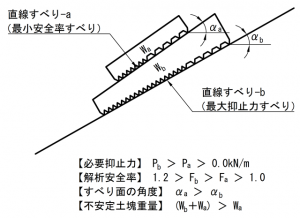
fig.-2 を参照してください。同図の上側のすべり a は,fig.-1 の最小安全率円弧すべり A を,直線すべりで表現し直したものです。同じく下側のすべり b は,fig.-1 の最大抑止力円弧すべり B を,直線すべりで表現したものです。直線すべり b は,「最大抑止力すべり」ですから,その必要抑止力は,直線すべり a よりも大きな値です。これについては,直線すべり b と直線すべり a の不安定土塊の大きさの違いから,直感的に理解していただけると思います。一方,安全率に関しては,直線すべり a が,直線すべり b よりも小さな値です。直線すべり a は,「最小安全率すべり」ですからね。ここで,安全率の定義式を思い出してください。安全率は,不安定土塊の滑動力とすべり面の摩擦抵抗力の比で定義されていましたよね。従って,不安定土塊の規模が小さくとも,すべり面の摩擦抵抗が小さければ,安全率が小さな値となってしまうことは,何ら不思議ではありません。
それでは,fig.-1 の円弧すべりモデルと,fig.-2 の直線すべりモデルの相違点は何でしょうか? すべり面の形状だけですよね。その他の,安全率,必要抑止力,すべり面の平均角度,および不安定土塊の重量など,すべり面形状以外の解析要素の大小関係は,全く同じです。すなわち,対策工を設計する上では,「直線すべり a:直線すべり b」の関係性と,「円弧すべり A:円弧すべり B」の関係性は,同じと考えて差し支えないはずです。
それでは,fig.-2 を認識していただいた上で,もう一度,先程の質問と解答例を思い出してください。
【問題】
fig.-2 の状況において抑止工を設計する場合,あなたは,抑止対象として,直線すべり a と直線すべり b のうち,どちらのすべりを採用しますか?
【誤解答】
直線すべり a の安全率が「最小安全率」なのだから,同すべりが最も危険なすべりであり,かつ最も早期に発生するすべりである。同すべりを抑止すれば,最大抑止力すべり b のような大規模な斜面崩壊が発生する前に,地盤の初期変状を抑えることができる。すなわち,最小安全率すべり a を対象とする抑止対策を施せば,最大抑止力すべり b を対象とする様な大規模な抑止対策を講じる必要はない。
ここで,想像力を働かせてください。解答例に従い,fig.-2 の直線すべり a に対して抑止工を配置してみましょう。最適設計でしょうか? “Slip Tips” にお付き合いいただいてきた読者の皆さんは,もうお察しのことと思いますが,敢えて説明します。直線すべり a の安全率は,抑止工を施すことで計画安全率を上回りますが,直線すべり b については,計画安全率が満たされる保証はありません。直線すべり b は,必要抑止力が最大となる「最大抑止力すべり」なのですから,この状況では概ね計画安全率は満たされていないと考えるべきでしょう。
すなわち,上記の解答例は「誤り」です。このままでは「過小設計」となってしまいます。ここで,ライズがご提案する正解例を以下に示します。
【正解例】
直線すべり b の必要抑止力が「最大抑止力」なのだから,同すべりを設計対象として抑止工を設計すべきである。最大抑止力すべり b を対象とする抑止対策を施せば,同すべりよりも必要抑止力が小さいすべりの安定は,十分に確保できる。
読者の皆さんは,「何言ってんだアンタ。誤解答の様な設計をする訳がないだろう。」と言われるかもしれません。ライズもそう思います。しかし,世間には,この種の設計がまかり通っているのが実情です。ライズの知る限りでは,特定の事業分野の設計成果の中に,この種の設計成果を時々見かけます。それらの報告書を読み解くと,前述の解答例のように「最適設計」であることを謳っているケース,「最大抑止力すべりの様な大規模な崩壊が発生する可能性は非常に低いので,最小安全率すべりを設計対象とする。」,あるいは「最大抑止力すべりを対象として設計した場合,対策工の規模が大きくなり過ぎ,当初に目論んでいた事業費を大きく上回ってしまうので,最小安全率すべりを設計対象とする。」などなど,信じられない理論が展開されています。ライズが照査をお引き受けした場合は,お客様に「過小設計」であることをお伝えしていますが,軒並み「有名なコンサルタント会社の設計成果なのだ! 権威ある先生様にお墨付きをいただいているのだ! 何の指摘もなく,会計検査をクリアーしているのだ! お前ごときが何言ってんだ!」的な雰囲気になってしまいます。設計業務が数年前に実施されたもので,既に対策工が施工済みであった場合などは,目も当てられません。「今さら,おかしなことを言わないでくれよ!」という気持ちになるのも,十分に理解できます。ですが,偉い先生がお墨付きを出されても,会計検査をクリアーした事業であったとしても,過小設計は過小設計です。想定内の雨や地震でさえ,斜面崩壊が発生する可能性があります。最悪の場合,尊い人命が失われてしまう可能性もあるのです。
以上の認識に基づいてライズが提案させていただく「最小安全率の利用上の留意点」は,以下の通りです。
「最小安全率すべりの必要抑止力を,斜面対策工の設計外力として利用してはならない。」
さらに,「円弧すべり試行計算の解析結果を利用する場合の留意点」として,以下の事柄を忘れないでください。
「極限平衡法に基づく斜面安定解析結果からは,すべりの発生順序や,すべりに隣接する地盤の不安定化などを推定することはできない。これらを推定するには,斜面の変状と時間経過に伴う変化を連立方程式でモデル化した,有限要素法,境界要素法,あるいは個別要素法などの解析手法を用いなけらばならない。」
・・・です。
【備考】
誤った解答例として考察した内容は,地すべり対策事業で採用される,「概成」→「完成」に至る長期計画に類似しています。これらの問題を同一視しないよう,留意してください。
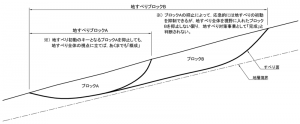
地形的あるいは地質的観点から,地すべりが小ブロックに分割されるようなケースでは,一部のブロックの安定を確保することによって,地すべり全体の初動をある程度抑えることがあります。fig.-3 に示すように,恒久対策としては,地すべりブロック B の対策が必要ですが,応急対策としては,地すべりブロック B を構成する小ブロック A の安定を図れば,ブロック B の滑動もある程度抑えられるようなケースです。大規模な地すべりにおいて,地すべり全体の安定に巨額な費用が必要とされる場合,小ブロック毎に対策を図りつつ,将来的には全体の安定を実現する,「概成」→「完成」に至る長期計画が採用されます。
ただし,このように,小ブロックの対策を繰り返す長期的な計画は,地すべりの滑動速度が遅く,不測の事態においても利用者を避難させることが可能な場合,かつ地すべりの移動量や移動速度などのモニタリングが十分に為されている場合に限って,初めて採用できる方法です。管理方針としてメンテナンスフリーを目指し,かつ崩壊土砂の移動速度が高速となる可能性が高い,道路法面や急傾斜地においては,適用が困難な方法です。
5. 次回の “Slip Tips” は,・・・
ブログテーマ「円弧すべり解析の最小安全率って何?」の投稿は,今回が最終回です。長らくお付き合いいただき,ありがとうございました。円弧すべり試行計算について,さらなる疑問のある方は,当該ウェブページの問い合わせフォームや,メール,あるいは電話などで,お気軽にお問い合わせください。
さて,次回の “Slip Tips” からは,新しい投稿テーマのスタートです。 乞うご期待!
平成27年1月23日 ライズ